北航计算机组成P0课下
北航计算机组成原理P0课下
P0课下做题的一些分享,思路不一定是最佳实现思路,敬请大家斧正
注意$logisim$的$Appearance$调整
P0.Q1 CRC校验码
读完了题目感觉题目和校验没什么关系
教程已经有了明显的提示,使用4位模2运算电路拼出11位的模2除法运算电路,考虑到本题应该是一个组合电路题,所以笔者使用了类似行波进位器的电路- 子电路定义如下(:sob:英语不好轻喷 )
定义接口 方向 描述 div[2:0] I 上一次$mod2$运算留下的余数 new I 本次$mod2$运算放在尾端的数 todiv[3:0] I 除数 hi[2:0] O 余数 lo O 商 - 有八次$mod2$运算所以实现了八个子电路$M_i ( 1 \le i \le 8)$
- 利用
Splitter分出后五位和三位零依次传入子电路中 - 连接$M_i.hi $ 与$ M_{i+1}.div$,就构成了行波$mod2$运算电路(
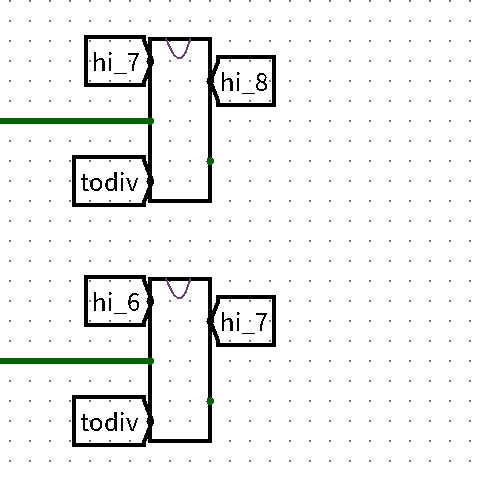
- 子电路定义如下(:sob:英语不好轻喷 )
- 其实本来看到$mod2$除法运算第一个想到的是循环移位,但是不知道能不能用时序,应该是不行吧
- 最后的最后,记得$Appearance$,记得$Appearance$,记得$Appearance$,重要的事情说三遍
P0.Q2 实现GRF
啊,是寄存器堆,我们完了
整体思路不难,输入数据使用32位DMX分配到各个寄存器,读出操作将寄存器堆连接32位MUX得到输出,最后的使能端口我使用了主的使能端$We$和各个寄存器的使能端$We_i$的综合
- $Attention$: 对于特殊寄存器
$0,我没有单独实现为一个寄存器,而是将写入$0的数据线置空,读取$0的数据线恒置为$0$
其实主要是搭建大量的寄存器和连接像上图的Tunnel容易导致莫名的连线问题,不过你可以CV,但是既然助教们在logisim教程中写了自动化教程肯定有他们的道理,所以我们用Python自动化脚本帮助我们生成GRF,感觉没我CV快是怎么回事 - 接下来构建
Python自动化脚本首先,既然要使用脚本生成大量的寄存器,我们就需要找到
GRF的最小单位,不然怎么愉快的for循环呢,大概是下面这样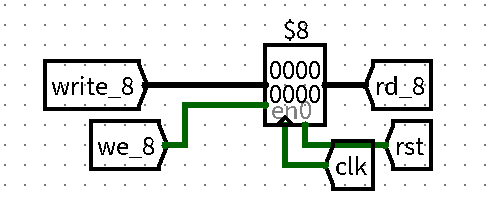
但是,我们观察logisim的电路文件,发现连线的操作很麻烦,是从一个坐标点导向另一个坐标点,坐标点嘛,如果写入脚本中,不仅会耗费大量时间记录需要连线的位置而且更易错,这违背了我们
图方便、省事的初衷<wire from="(340,890)" to="(430,890)"/>
<wire from="(70,1050)" to="(100,1050)"/>
<wire from="(70,1070)" to="(100,1070)"/>
<wire from="(70,250)" to="(130,250)"/>所以我们对上述电路进行如下改造,丑是丑了点,但是
XML格式十分简洁,反正logisim文件不是给人看的,机器看得明白就行
<comp lib="4" loc="(500,320)" name="Register">
<a name="width" val="32"/>
<a name="label" val="$18"/>
</comp>
<comp lib="0" loc="(330,340)" name="Tunnel">
<a name="label" val="clk"/>
</comp>
<comp lib="0" loc="(480,340)" name="Tunnel">
<a name="label" val="clk"/>
</comp>
<comp lib="0" loc="(320,395)" name="Tunnel">
<a name="facing" val="east"/>
<a name="width" val="32"/>
<a name="label" val="write_11"/>
</comp>
<comp lib="0" loc="(500,620)" name="Tunnel">
<a name="width" val="32"/>
<a name="label" val="rd_22"/>
</comp>
<comp lib="0" loc="(180,565)" name="Tunnel">
<a name="label" val="clk"/>
</comp>
<comp lib="0" loc="(500,395)" name="Tunnel">
<a name="width" val="32"/>
<a name="label" val="rd_19"/>
</comp>
<comp lib="0" loc="(630,640)" name="Tunnel">
<a name="label" val="clk"/>
</comp>因为原电路已经略显复杂,接下来我单开了一个circuit搭建了一个最小单位,然后就能比较方便地找到这个基本单位了,接下来就是使用Python生成xml文件了,我使用的源码如下
grf = """ <comp lib="4" loc="%s" name="Register">
<a name="width" val="32"/>
<a name="label" val="%s"/>
</comp>
<comp lib="0" loc="%s" name="Tunnel">
<a name="width" val="32"/>
<a name="label" val="%s"/>
</comp>
<comp lib="0" loc="%s" name="Tunnel">
<a name="facing" val="east"/>
<a name="label" val="%s"/>
</comp>
<comp lib="0" loc="%s" name="Tunnel">
<a name="label" val="rst"/>
</comp>
<comp lib="0" loc="%s" name="Tunnel">
<a name="label" val="clk"/>
</comp>
<comp lib="0" loc="%s" name="Tunnel">
<a name="facing" val="east"/>
<a name="width" val="32"/>
<a name="label" val="%s"/>
</comp>
"""
row = 150
col = 75
with open("grf.xml", "w", encoding="utf-8") as file:
for i in range(4):
for j in range(8):
reg_loc = [200 + i * row, 170 + j * col]
grf_name = f"${i * 8 + j }"
rd_name = f"rd_{i * 8 + j }"
rd_loc = reg_loc
we_loc = [reg_loc[0] - 30, reg_loc[1] + 10]
we_name = f"we_{i * 8 + j }"
rst_loc = [reg_loc[0] - 10, reg_loc[1] + 20]
clk_loc = [reg_loc[0] - 20, reg_loc[1] + 20]
wri_loc = [reg_loc[0] - 30, reg_loc[1]]
wri_name = f"write_{i * 8 + j }"
# print(grf % (tuple(reg_loc), grf_name, tuple(rd_loc), rd_name, tuple(we_loc), we_name,tuple(rst_loc), tuple(clk_loc), tuple(wri_loc), wri_name))
file.write(grf % (tuple(reg_loc), grf_name, tuple(rd_loc), rd_name, tuple(we_loc), we_name,tuple(rst_loc), tuple(clk_loc), tuple(wri_loc), wri_name))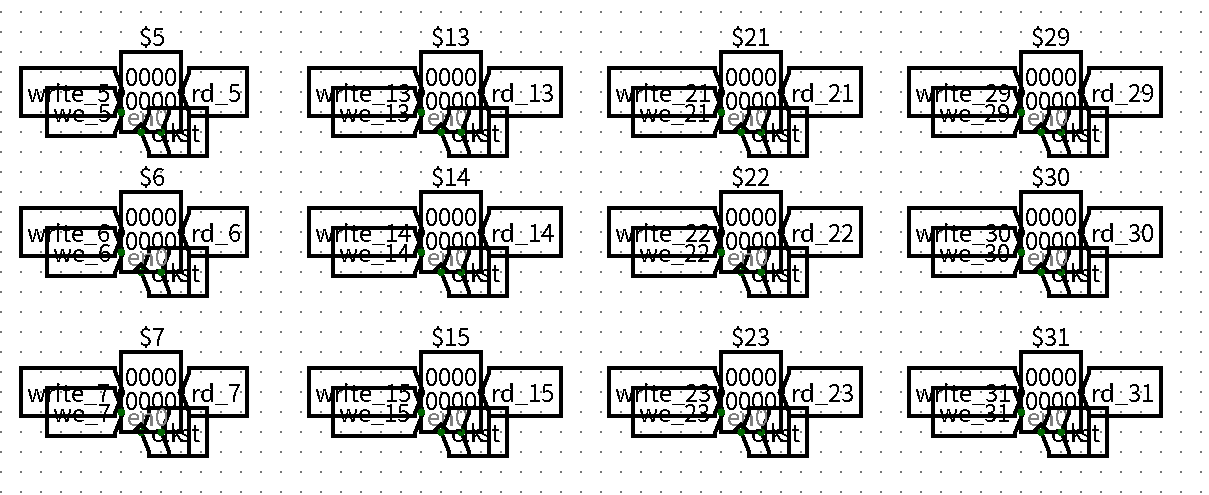
(大概是这样,间距还可以调整,修改代码中的row和col值即可)
对于连接
MUX与DMX我们如法炮制,新开一个文件存放最小单位,这里的最小单位其实是就是自己,只是连接的32个Tunnel还是有规律的<comp lib="2" loc="(560,250)" name="Demultiplexer">
<a name="select" val="5"/>
<a name="width" val="32"/>
<a name="enable" val="false"/>
</comp>
<comp lib="0" loc="(520,10)" name="Tunnel">
<a name="label" val="write_1"/>
</comp>
<comp lib="0" loc="(520,20)" name="Tunnel">
<a name="label" val="write_2"/>
</comp>发现在$y=250$位置的DMX的第一个接口时从0开始的,每两个接口之间是10个单位,就可以使用for循环生成这些
Tunnel了,源码如下mux_1 = """
<comp lib="2" loc="(250,250)" name="Multiplexer">
<a name="select" val="5"/>
<a name="width" val="32"/>
<a name="enable" val="false"/>
</comp>"""
mux_2 = """
<comp lib="2" loc="(430,250)" name="Multiplexer">
<a name="select" val="5"/>
<a name="width" val="32"/>
<a name="enable" val="false"/>
</comp>"""
mux_loc = [(250, 250), (430, 250)]
tunnel_rd = """
<comp lib="0" loc="%s" name="Tunnel">
<a name="facing" val="east"/>
<a name="width" val="32"/>
<a name="label" val="%s"/>
</comp>"""
dmx = """
<comp lib="2" loc="(560,250)" name="Demultiplexer">
<a name="select" val="5"/>
<a name="enable" val="false"/>
</comp>"""
dmx_loc = (560, 250)
tunnel_wr = """
<comp lib="0" loc="%s" name="Tunnel">
<a name="label" val="%s"/>
</comp>"""
with open("mux.xml", "w", encoding="utf-8") as file:
for z in range(2):
for i in range(32):
tun_loc = [mux_loc[z][0] - 40, 90 + 10 * i]
tun_name = f"rd_{i}"
print(tunnel_rd % (tuple(tun_loc), tun_name))
file.write(tunnel_rd % (tuple(tun_loc), tun_name))
file.write(mux_1)
file.write(mux_2)
file.write(dmx)
for i in range(32):
tun_loc = [dmx_loc[0] + 40, 90 + 10 * i]
tun_name = f"we_{i}"
print(tunnel_wr % (tuple(tun_loc), tun_name))
file.write(tunnel_wr % (tuple(tun_loc), tun_name))
# 这里本来有一个写WD的write的for循环,图方便注释掉了
# 只需要把tun_name自行调整即可,记得是DMX哦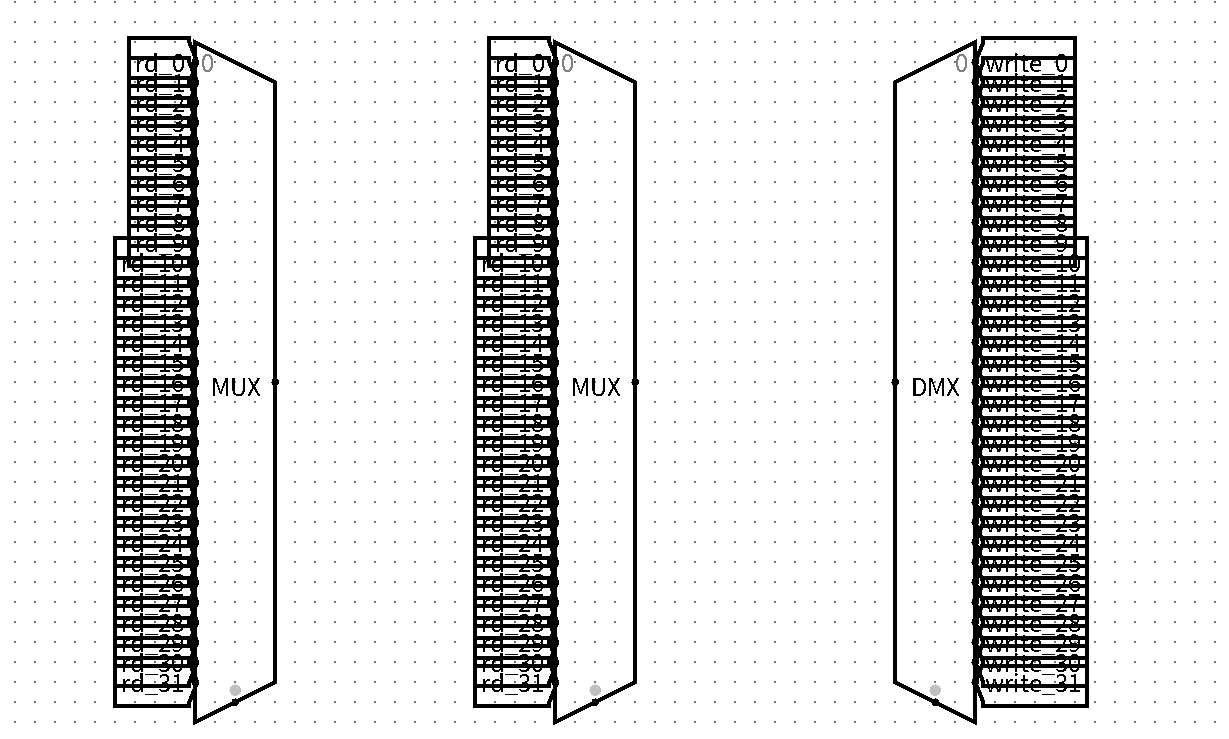
- 这个题目好,P4写单周期的时候还能用
GRF,巨能用,一节更比六节强,玩具车用完收音机还能用- 最后的最后,记得$Appearance$,记得$Appearance$,记得$Appearance$,重要的事情说三遍(你怎么知道我$Pre$ 被$Appearance$卡到④了)
P0.Q3 导航
爵士好题刚开始看到这道题本来打算用
Mealy机,使用Mealy机真的很方便,因为hit和arrive都与status、dir有关,但是因为题目指定了Moore机所有很快就丢弃了这个思路然后想到了创建多个状态包括撞墙的状态,然后写出复杂的状态转移方程,最后一共有13个状态吧,构建状态转移方程过于复杂,所以也丢弃了
最后我还是决定使用
Mealy状态机和Register构建一个Moore状态机(假装输出只和状态相关)Register保存hit的值,使得hit只在时钟上升沿变化,看起来就像是只随着status变化了(因为status是随着时钟上升沿变化的),而arrive本身就可以只与status有关,那么我们关于status的Moore机就构建好了
状态转移的真值表如下
status dir next_status arrive hit 000 00 001 0 0 000 01 000 0 1 000 10 000 0 1 000 11 000 0 1 001 00 011 0 0 001 01 010 0 0 001 10 000 0 0 001 11 001 0 1 010 00 100 0 0 010 01 010 0 1 010 10 010 0 1 010 11 001 0 0 011 00 011 0 1 011 01 100 0 0 011 10 001 0 0 011 11 011 0 1 100 ?? 000 1 0 主电路图大致如下
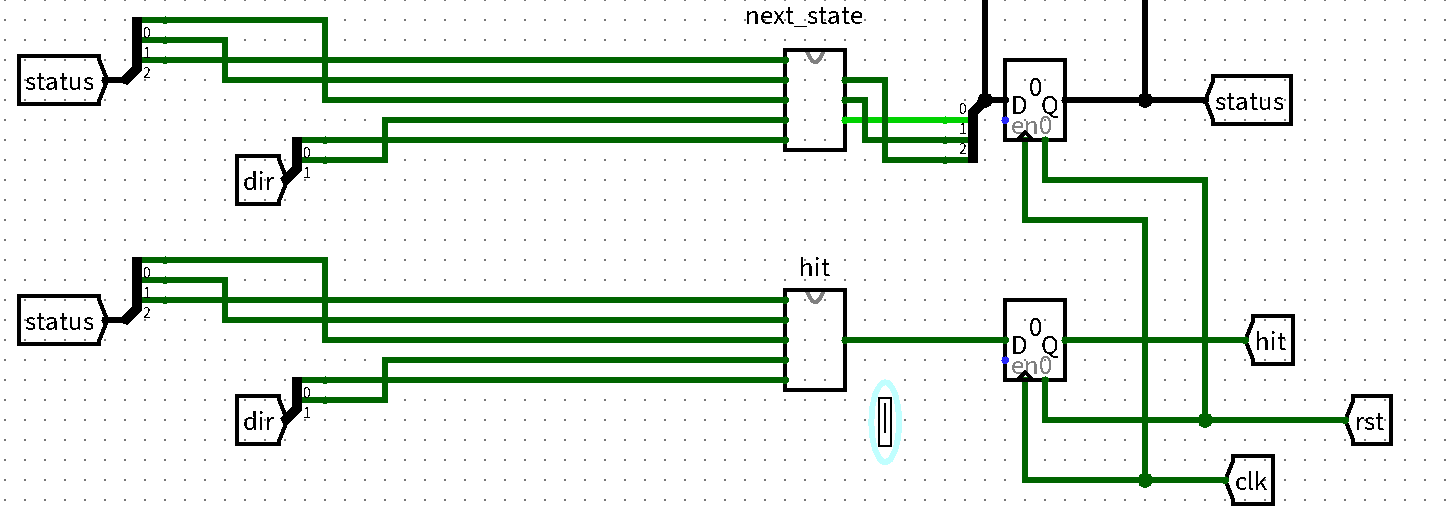
在群里看到向巨只用了两位的
type,我也想了一下,下面是我的思路- 相较于原本的电路,将状态
100即在B机房这个状态去除,改为在S2状态下dir为01、S3状态下dir为00时,arrive置1,且返回A机房(Mealy状态机 + 寄存器) arrive模块也使用Register保存,在时钟上升沿更新- 在A机房状态下,如果
arrive为1,则总状态不更新,类似于同步复位信号,不过status这个时候已经是00
- 相较于原本的电路,将状态
向巨,yyds
P0.Q4 正则表达式
欸,这道题没有$Q3$难欸,怎么放在$Q4$
好了回归题目,这次的题目是一个Mealy类型的有限状态机,所以千万不要写错成了Moore类型的状态机啊主要就是
Moore状态机会比Mealy状态机多一个状态,因为Moore状态机保存了最后匹配成功的一个状态,Mealy状态机不需要保存匹配成功的状态,只需要在输入最后匹配条件时输出$1$,并且回到非法状态即可Mealy状态机状态转移图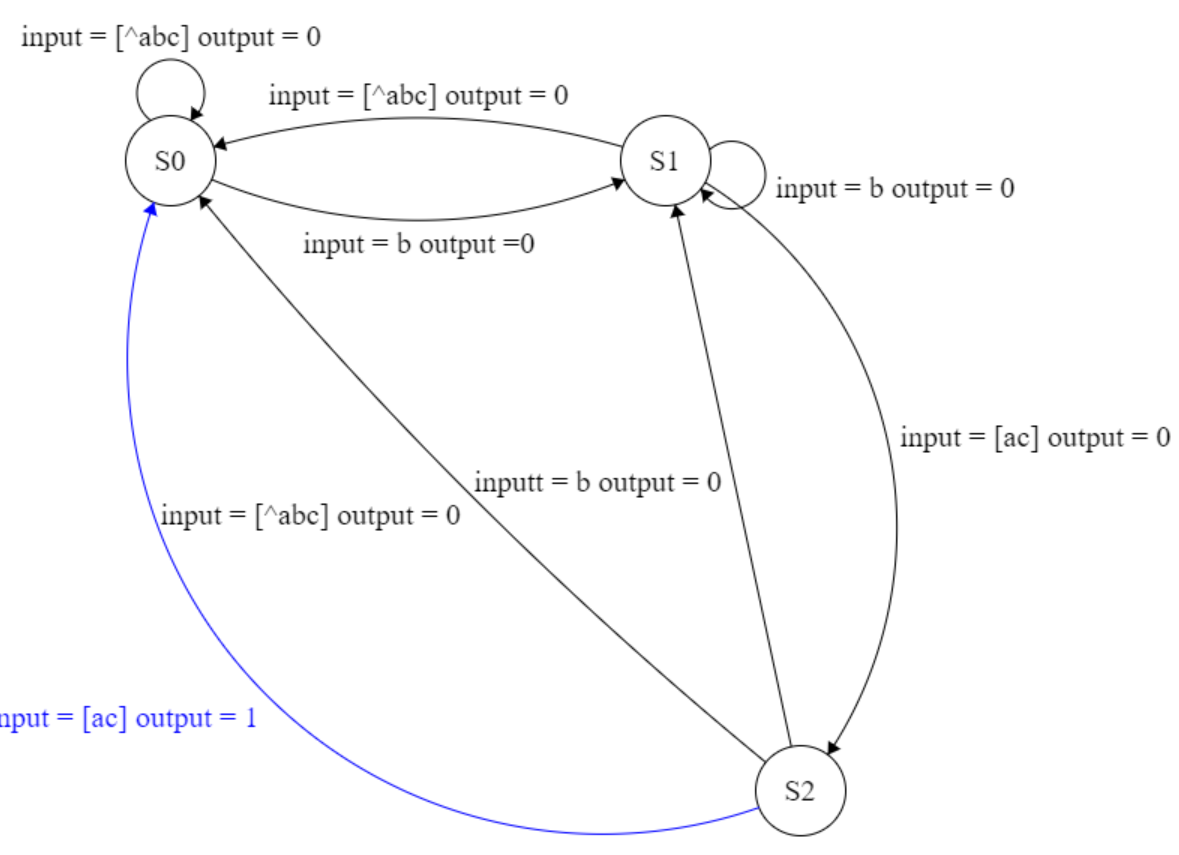
Moore状态机状态转移图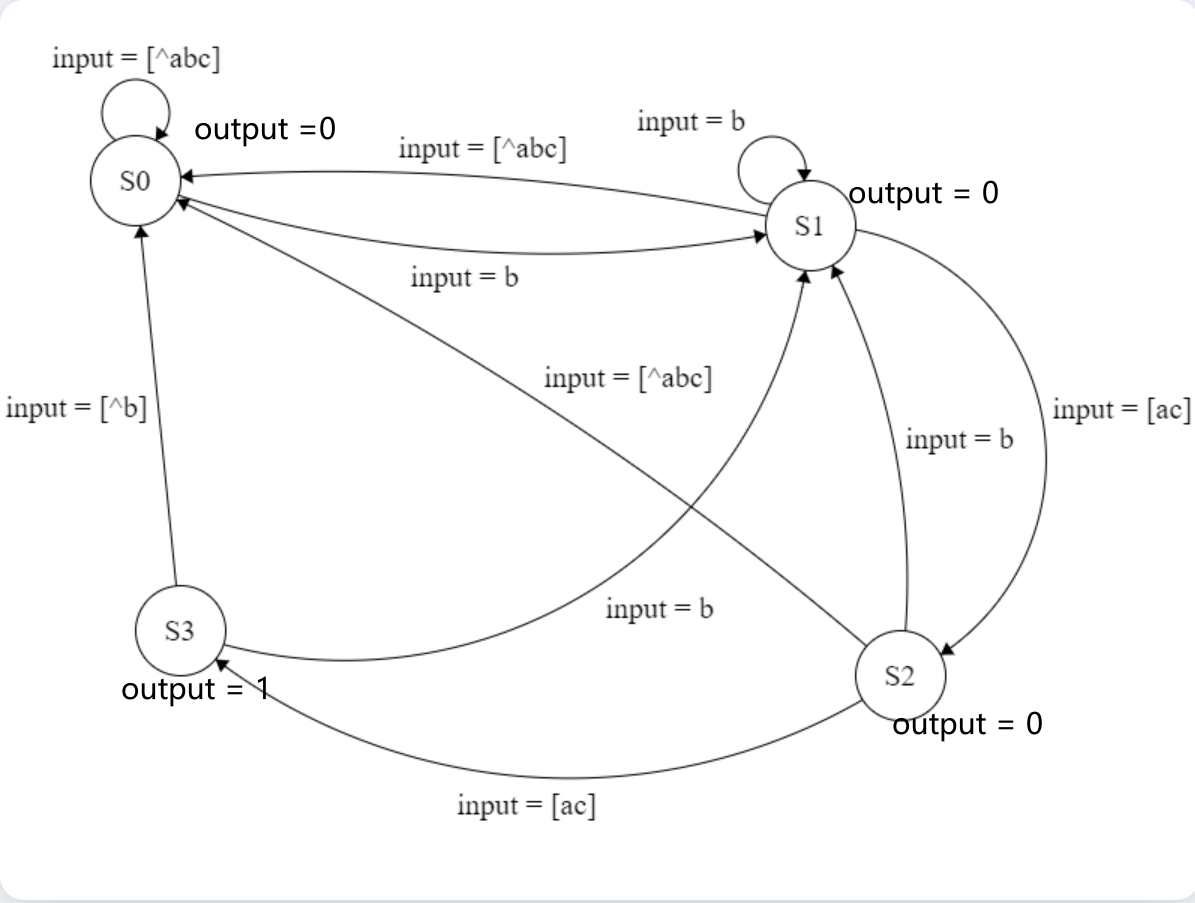
Mealy状态机状态转移方程status input next_status output 00 00 00 0 00 01 01 0 00 10 00 0 00 11 00 0 01 00 10 0 01 01 01 0 01 10 10 0 01 11 00 0 10 00 00 1 10 01 01 0 10 10 00 1 10 11 00 0
P0.附加题 ftoi
半精度浮点数,所以不能用C语言编测试数据了,助教很坏根据题目改编的IEEE浮点数,我们大致可以分为四类
- $规格化小数$
- $非规格化小数$
- $0$
- $\infty$
- $NAN$
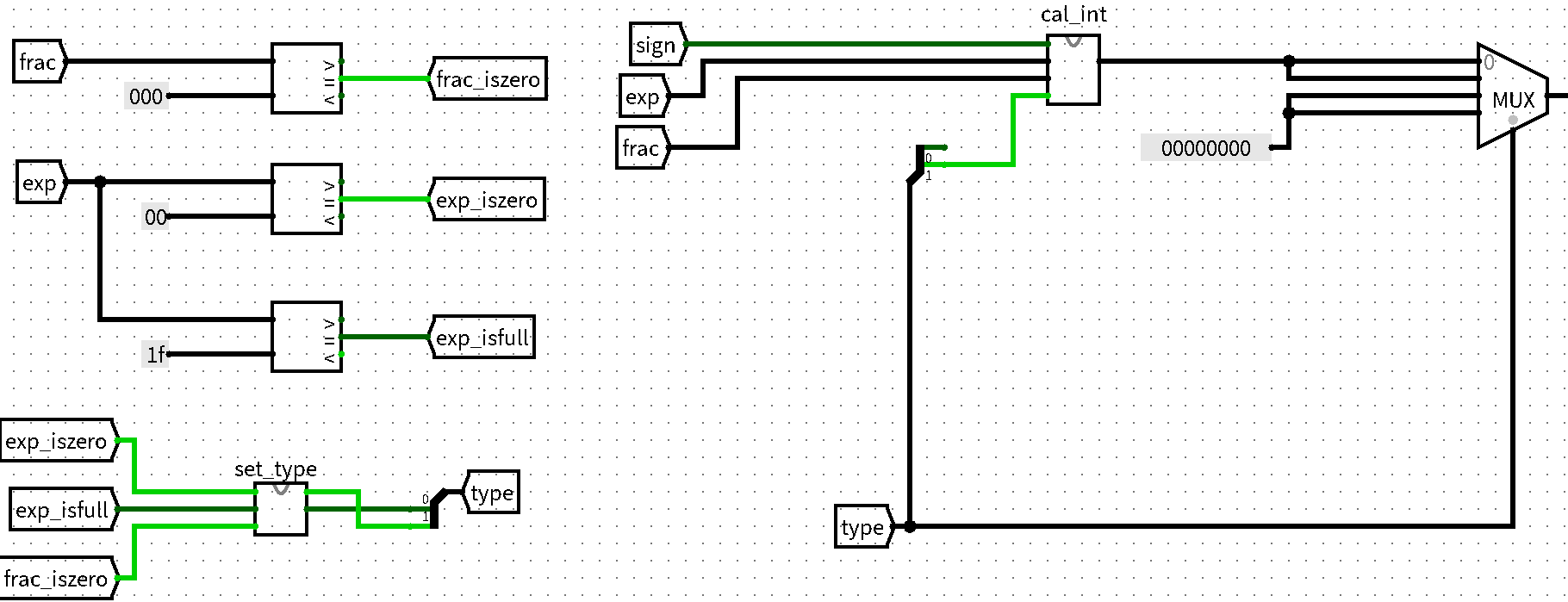
浮点数的类型又可以由下面三个bool型变量决定
exp_iszeroexp_isfullfrac_iszero
$NAN$ 和 $\infty$只有
frac_iszero不一致,又因为刚好有5个类型,所以干脆将这两个类型合并为一个,然后使用真值表技术生成两位type关于三个变量的子电路定义接口 方向 描述 exp_iszero I 所得浮点数exponent位置是否全为0 exp_isfull I 所得浮点数exponent位置是否全为1 frac_iszero I 所得浮点数fraction位置是否全为0 type[1:0] O 浮点数属于的类型 - 状态转移真值表如下
exp_iszero exp_isfull frac_iszero type 0 0 0 00 1 0 0 01 1 0 1 10 0 1 ? 11
- 状态转移真值表如下
后两个类型的输出都是$0$,前两个类型的唯一区别是
frac定点数的小数点前是否有默认的$1$,所以先讲述而这在实现上的共性- 通过
exponent的值和bias的值算出真正需要的位移值shift(补码编码),这里使用加法电路实现减法电路不用考虑溢出,这得益于移码中bias选择(一般是$\lfloor exp_{max} /2 \rfloor$) - 如果
shift是负数,则直接输出$0$即可,因为$0 \lt frac \lt 2$,所以至多右移$1$位就直接为$0$ - 我通过
shift与$10$比较直接决定左移还是右移,好处是不需要考虑先左移shift再右移$10$可能导致的高位$1$损失,坏处是又要写两个减法电路(,然后再MUX选择结果 - 根据
sign符号位决定是否取反加1,同样不需要考虑溢出
- 通过
接下来分别说明两次可以忽略溢出的原因(
有点废话的证明)- 对于第一个算的
shift(补码编码),主要原因是非符号数的减法电路和符号数的减法电路实际是一套电路,而且bias设置的好,如果exponent的首位是0,我们理解为补码的减法电路,正数减去正数不会溢出,得到的答案(补码是正确的),如果exponent的首位是1,因为bias设置的合理,只有11111的情况会无法得到正数,但是这种情况已经被排除了(因为其他的type使用了),所以得到的补码也是正确的(正数的编码是自己) - 第二个负数取补码的情况时,为什么不需要考虑可能已经溢出到32位外的值,取完补码再取后32位,而是直接不考虑开始时的溢出,这和一个小结论有关,对于一个正数取其相反数的补码可以这样做:从这个正数最低位的1开始,到最高位为止中间的所有数字取反,假设1全部溢出在32位外,则后32位始终保持0,假设后32位中有1,根据结论无论考不考虑溢出部分后32位的值都应该一致的
- 对于第一个算的
P0.推荐题目
好,但是现在还没出









